Bitcoin Programming: Elliptic Curves Equation

Back to the basic of the Ellipctic Curves equation.

I am curious how the equation works, the log discrete problem. Thus i decide to write

it in this blog of my own. The thing is, given public point could be recalculate and return

the same x-coordinate.

Point Addition

Elliptic curves are useful because of something called point addition. Point addition is where we can do an operation on two of the points on the curve and get a third point, also on the curve. This is called addition because the operation has a lot of the intu‐ itions we associate with the mathematical operation of addition. For example, point addition is commutative. That is, adding point A to point B is the same as adding point B to point A. 

Quote from the book. Yes, this is one the properties that interesting. One can add 2 points on the curve and the product is also on curve.

The other properties of the addition itself, is nonlinear. This is rings the bell that hashing supposedly one-way process.

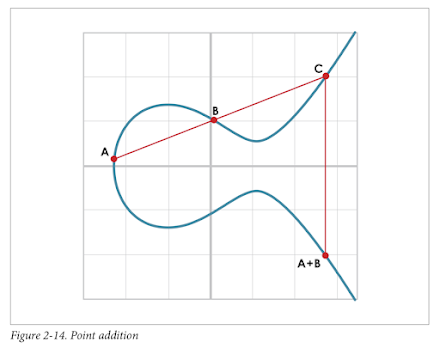
One of the properties that we are going to use is that point addition is not easily pre‐ dictable. We can calculate point addition easily enough with a formula, but intuitively, the result of point addition can be almost anywhere given two points on the curve. Going back to Figure 2-14, A + B is to the right of both points, A + C would be some‐ where between A and C on the x-axis, and B + C would be to the left of both points. In mathematics parlance, point addition is nonlinear. 

Conclusion:

The formula of the elliptic covered or bundled with the book, would cek if the X,Y point is on-curve.

The addition of two-points that on-curved would result a point somewhere in the curve.

There are also some properties that needs to be covered such-as when
a. Points X1 != X2

b. Points of X1 is equal to the Point of X2, P1 == P2

c. Points of X1 is equal to the Point of X2 , where y is 0